causens: an R package for causal sensitivity analysis methods • causens

Introduction

Methods to estimate causal quantities often rely no unmeasured confounding. However, in practice, this is often not the case. causens is an R package that provides methods to estimate causal quantities in the presence of unmeasured confounding. In particular, causens implements methods from the three following school of thoughts:

Frequentist methods based on sensitivity functions
Bayesianism via parametric modelling
Monte Carlo sensitivity analysis (TBA)

All implemented methods are accessible via the causens function with the method parameter. The package also provides a simulate_data function to generate synthetic data on which to test the methods.

Installation

The package can be installed from GitHub via devtools.

library(devtools)
#> Loading required package: usethis
devtools::install_github("Kuan-Liu-Lab/causens")
#> Using github PAT from envvar GITHUB_PAT. Use `gitcreds::gitcreds_set()` and unset GITHUB_PAT in .Renviron (or elsewhere) if you want to use the more secure git credential store instead.
#> Downloading GitHub repo Kuan-Liu-Lab/causens@HEAD
#> ── R CMD build ─────────────────────────────────────────────────────────────────
#> * checking for file ‘/tmp/RtmpUMPWq6/remotes1a5d5c998db0/Kuan-Liu-Lab-causens-d5727cf/DESCRIPTION’ ... OK
#> * preparing ‘causens’:
#> * checking DESCRIPTION meta-information ... OK
#> * checking for LF line-endings in source and make files and shell scripts
#> * checking for empty or unneeded directories
#> * building ‘causens_0.0.2-9000.tar.gz’
#> Installing package into '/home/runner/work/_temp/Library'
#> (as 'lib' is unspecified)

Methods

Summary of the Unmeasured Confounder Problem

In causal inference, the potential outcome framework is often used to define causal quantities. For instance, if a treatment $Z$ is binary, we respectively define $Y(1)$ and $Y(0)$ as the outcomes under treatment and control as if we can intervene on them a priori. However, in observational settings, this is often not the case, but we can still estimate estimands, e.g. the average treatment effect $\tau = \mathbb{E}[Y(1) - Y(0)]$ , using observational data using causal assumptions that relate potential outcome variables to their observational counterpart:

Consistency: $Y = Y(1)Z + Y(0)(1 - Z)$
Conditional exchangeability: $Y(1), Y(0) \perp Z | X$
Positivity: $0 < P(Z = 1 | X) < 1$

where $X$ is a set of observed confounders that can be used to adjust for confounding. In practice, it is often difficult to know whether these assumptions hold, and in particular, whether all confounding variables are contained in $X$ .

Hereon, we define $U$ , the set of unmeasured confounders, although, in causens, we assume $U$ to be univariate for simplicity.

Simulated Data Mechanism

We posit the following data generating process:

$\begin{align*} X_1 &\sim \text{Normal}(0, 1) \\ X_2 &\sim \text{Normal}(0, 1) \\ X_3 &\sim \text{Normal}(0, 1) \\ U &\sim \text{Bern}(0.5) \\ Z &\sim \text{Bern}(\text{logit}^{-1}(\alpha_{uz} U + \alpha_{xz} X_3)) \\ Y1 &\sim \text{Normal}(\beta_{uy} U + 0.5 X_1 + 0.5 X_2 - 0.5 X_3) \\ Y0 &\sim \text{Normal}(0.5 X_1 + 0.5 X_2 - 0.5 X_3) \, . \end{align*}$

Using consistency, we define $Y = Y_1 Z + Y_0 (1 - Z)$ . Note that, in simData.R, we provide some options to allow the simulation procedure to be more flexible. Parameters $\alpha_{uz}$ and $\beta_{uy}$ dictate how the unmeasured confounder $U$ affects the treatment $Z$ and the outcome $Y$ , respectively; by default, they are set to 0.2 and 0.5.

Frequentist Methods (Brumback et al. 2004, Li et al. 2011)

Building on the potential outcome framework, the primary assumption that requires adjustment is conditional exchangeability. First, the latent conditional exchangeability can be articulated as follows to include $U$ :

$\begin{align*} Y(1), Y(0) \perp Z | X, U \end{align*}$

Secondly, we can define the sensitivity function $c(z, e)$ , with $z$ being a valid treatment indicator and $e$ being a propensity score value.

$\begin{align*} c(z, e) = \mathbb{E}\Big[Y(z) \mid Z = 1, e\Big] - \mathbb{E}\Big[Y(z) \mid Z = 0, e\Big] \end{align*}$

When there are no unmeasured confounders, $c(z, e) = 0$ for all $z$ and $e$ since $U = \emptyset$ .

Given a valid sensitivity function, we can estimate the average treatment effect via a weighting approach akin to inverse probability weighting.

For parsimony, we provide an API for constant and linear sensitivity functions, but we eventually will allow any valid user-defined sensitivity function.

# Simulate data
data <- simulate_data(
  N = 10000, seed = 123, alpha_uz = 1,
  beta_uy = 1, treatment_effects = 1
)

# Treatment model is incorrect since U is "missing"
causens(Z ~ X.1 + X.2 + X.3, "Y", data = data, method = "Li", c1 = 0.25, c0 = 0.25)
#> $estimated_ate
#> [1] 1.005025
#> 
#> $call
#> Z ~ X.1 + X.2 + X.3
#> 
#> attr(,"class")
#> [1] "causens_sf"

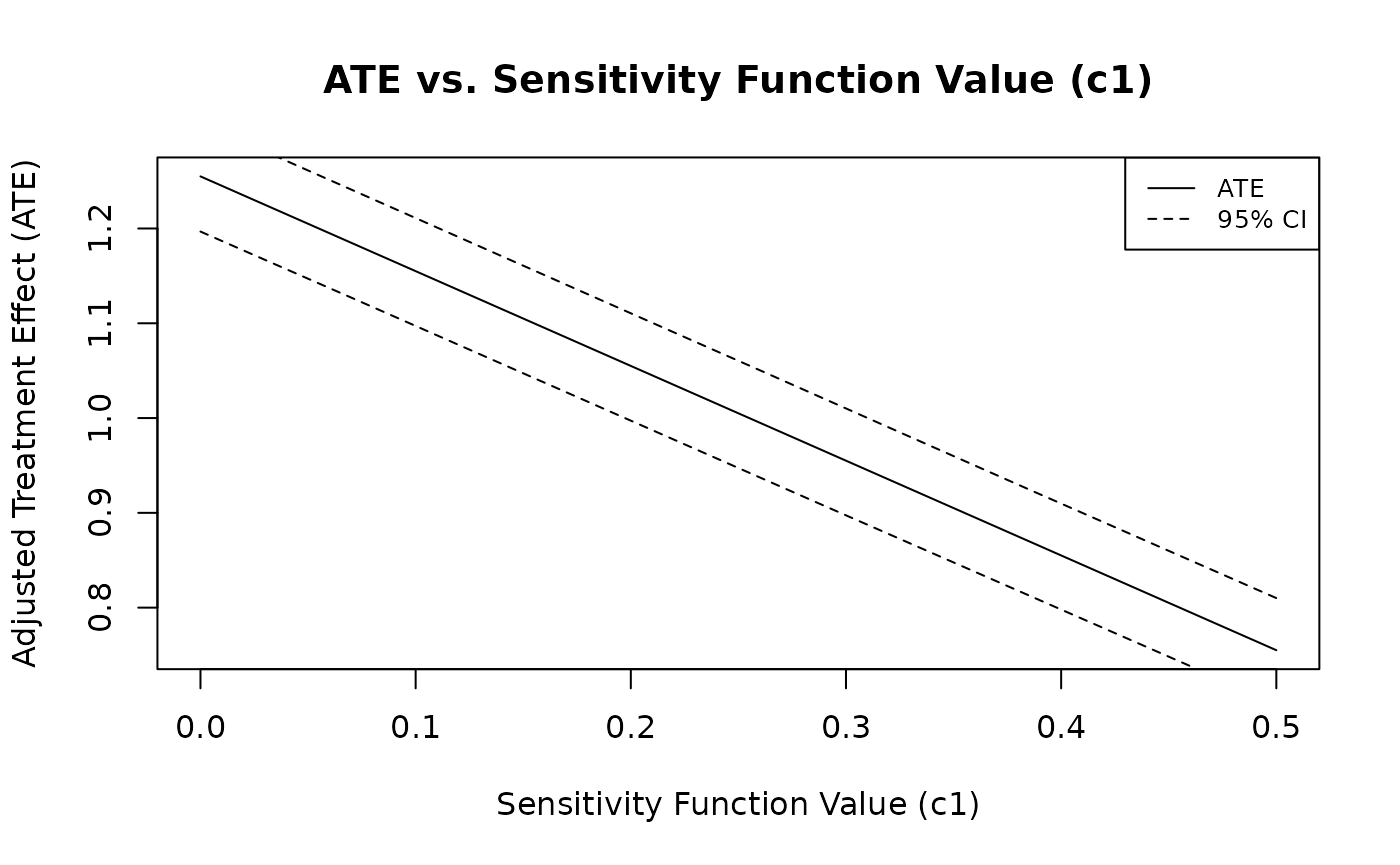
Bayesian Methods

In Bayesianism, we can adjust for unmeasured confounding by explicitly modelling $U$ and its relationship with $Z$ and $Y$ . Using a JAGS backend to carry out the MCMC procedure, we can estimate the average treatment effect by then marginalizing over $U$ . We assume the following data-generating mechanism and Bayesian model in causens:

$\begin{align*} X_1, X_2, X_3 &\stackrel{iid}{\sim} \text{Normal}(0, 1) \\ U \mid X &\sim \operatorname{Bern}\left(\text{logit}^{-1}\gamma_{ux} X\right) \\ Z \mid U, X &\sim \text{Bern}\left(\text{logit}^{-1}(\alpha_{uz} U + \alpha_{xz} X)\right) \\ Y \mid U, X, Z &\sim \text{Normal}(\beta_{uy} U + \beta_{xy} X + \tau Z) \\ \end{align*}$

data <- simulate_data(
  N = 1000, alpha_uz = 0.5, beta_uy = 0.2,
  seed = 123, treatment_effects = 1,
  y_type = "continuous"
)

causens(Z ~ X.1 + X.2 + X.3, "Y", data, method = "Bayesian")

Monte Carlo Approach to Causal Sensitivity Analysis

Warning Only works for binary outcomes, for now.

The Monte Carlo approach proceeds through the following steps:

Produce a “naive” model where $U$ is ignored: $\text{logit}\Big(P(Y = 1 \mid Z, X)\Big) = \beta_0 + \beta_Z Z + \beta_X X$ .
With estimates $\widehat{\beta}_Z$ and $\widehat{\text{SD}}(\widehat{\beta}_Z)$ of $\beta_Z$ and $\text{SD}(\widehat{\beta}_Z)$ obtained from fitting the naive model, we can sample $\beta_U, \gamma_0, \gamma_Z$ from an assumed prior distribution: $\begin{align*} \beta_U &\sim \text{Uniform}(-2, 2) \\ \gamma_0 &\sim \text{Uniform}(-5, 5) \\ \gamma_Z &\sim \text{Uniform}(-2, 2) \, . \end{align*}$
For each sample $\left(\beta_U^{(r)}, \gamma_0^{(r)}, \gamma_Z^{(r)}\right)$ indexed by $r = 1, \dots, R$ , we can compute bias adjusted $\widehat{\beta}_Z^{(r)}$ estimates: $\widehat{\beta}_Z^{(r)} = \widehat{\beta}_Z - \log \left(\frac{(1 + \exp(\beta_U^{(r)} + \gamma_0^{(r)} + \gamma_X^{(r)}))(1 + \exp(\gamma_0^{(r)}))}{(1 + \exp(\beta_U^{(r)} + \gamma_0^{(r)}))(1 + \exp(\gamma_0^{(r)} + \gamma_X^{(r)}))}\right)$
Finally, we can sample the bias adjusted average treatment effect estimate $\beta^{(r)} \sim \text{Normal}\left(\widehat{\beta}_Z^{(r)}, \widehat{SD}\left(\widehat{\beta}_Z\right)^2\right)$ to account for errors incurred in previous steps. With $\beta^{(1)}_Z, \dots, \beta^{(R)}_Z$ , we can compute the Monte Carlo estimate of the average treatment effect by taking their average.

data <- simulate_data(
  N = 1000, alpha_uz = 0.2, beta_uy = 0.5,
  seed = 123, treatment_effects = 1, y_type = "binary",
  informative_u = FALSE
)

causens(Z ~ X.1 + X.2 + X.3, "Y", data, method = "Monte Carlo")
#> $call
#> Z ~ X.1 + X.2 + X.3
#> 
#> $estimated_ate
#> [1] 0.9929688
#> 
#> $std_error
#> [1] 0.3198489
#> 
#> $ci
#>      2.5%     97.5% 
#> 0.3060208 1.6760731 
#> 
#> attr(,"class")
#> [1] "monte_carlo_causens"